자료구조 - 트리
트리
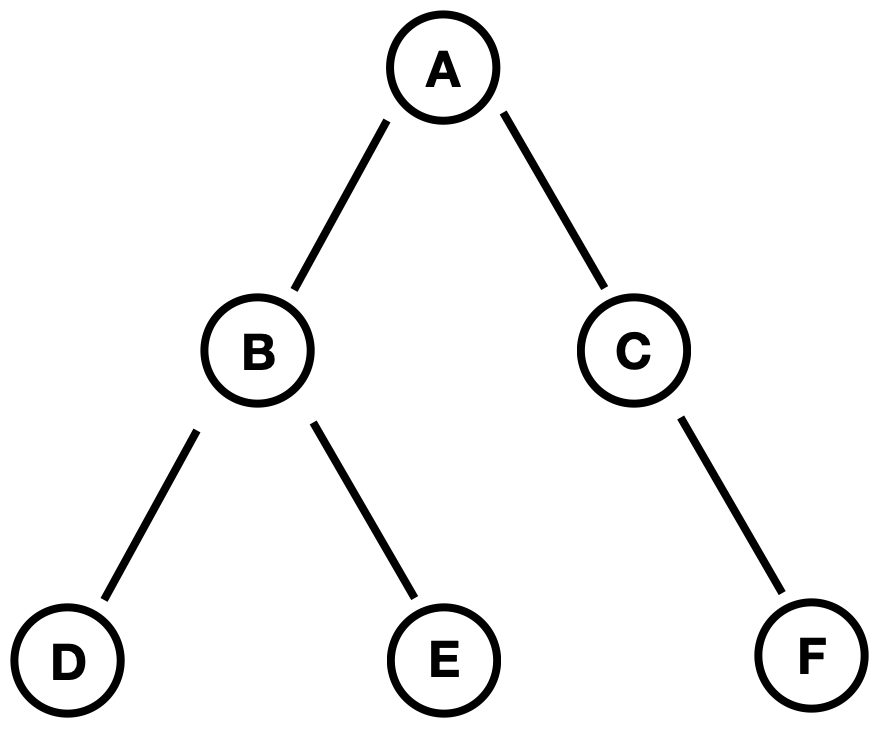
트리는 비선형구조로 데이터를 아래 그림처럼 계층적으로 저장하는 방법입니다. 선형구조자료와 달리 단순한 데이터 저장이 아닌, 계층적 관계를 표현하기 위해 데이터가 저장됩니다. 이 그림에서 트리 관련 용어에 대해 살펴보겠습니다.
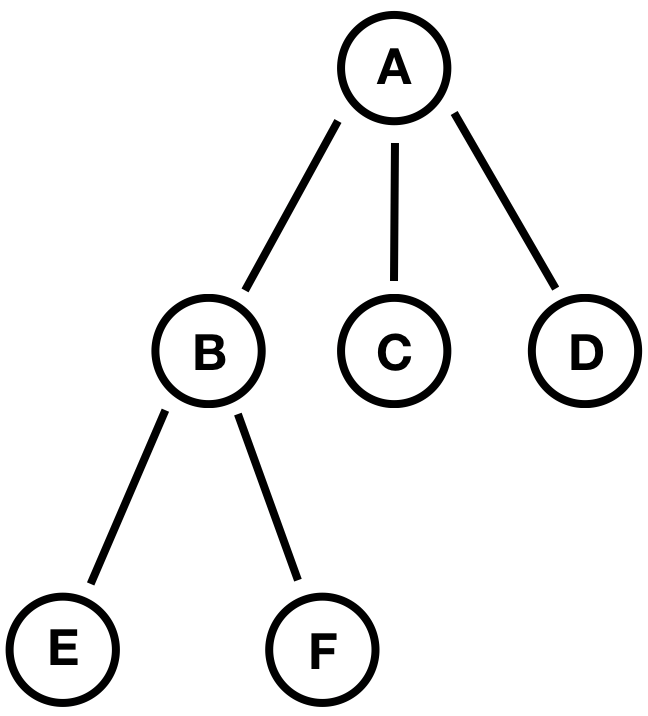
- 노드(Node) : 트리의 마디점 (A, B, C, D, E, F)
- 간선(Edge) : 노드와 노드끼리 연결하는 선
- 루트 노드(Root Node) : 최상위 노드 (A)
- 단말 노드(Terminal Node) : 하위 노드가 없는 노드 (C, D, E, F)
- 내부 노드(Internal Node) : 단말 노드를 제외한 노드 (A, B)
일반 트리
예시
- DOM
- File System
• 빅오
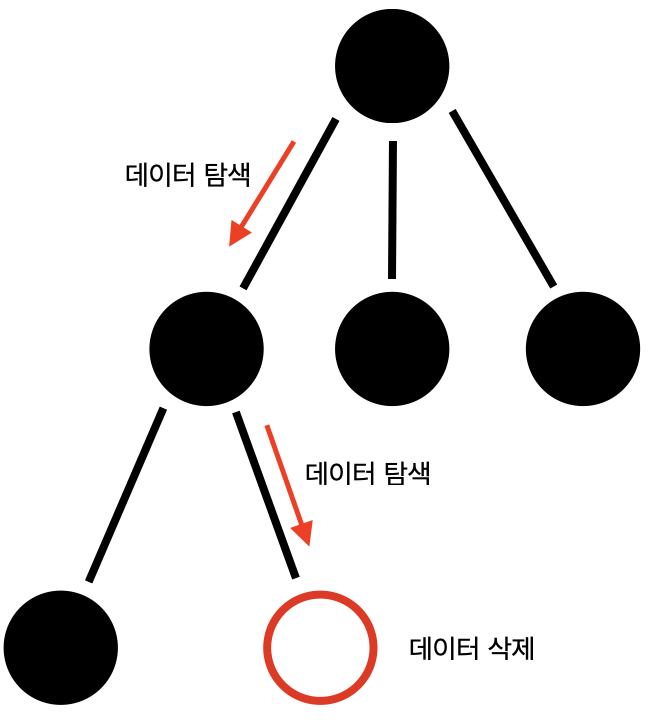
트리의 삽입/탐색/삭제의 빅오에 대해 알아보겠습니다. 아래는 트리를 보여주며, 어떤 값이 들어있는지 모릅니다.
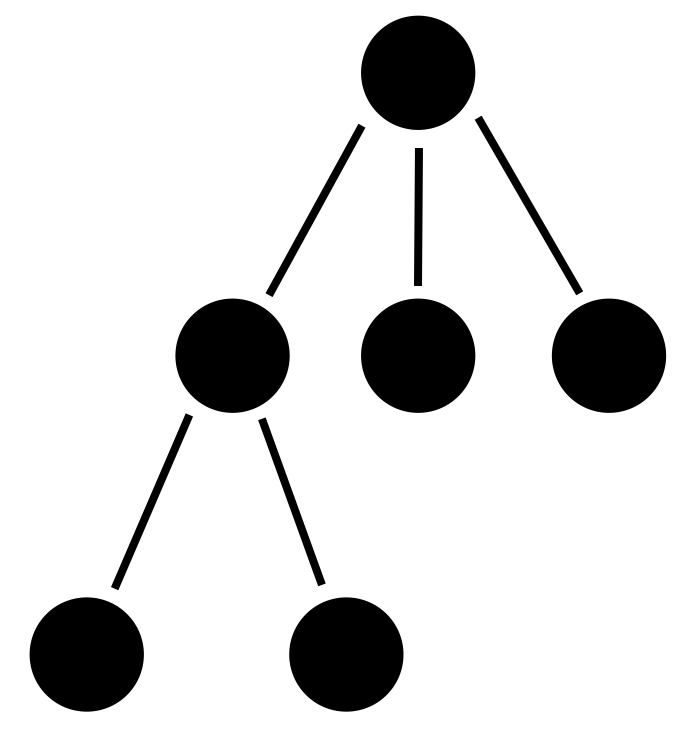
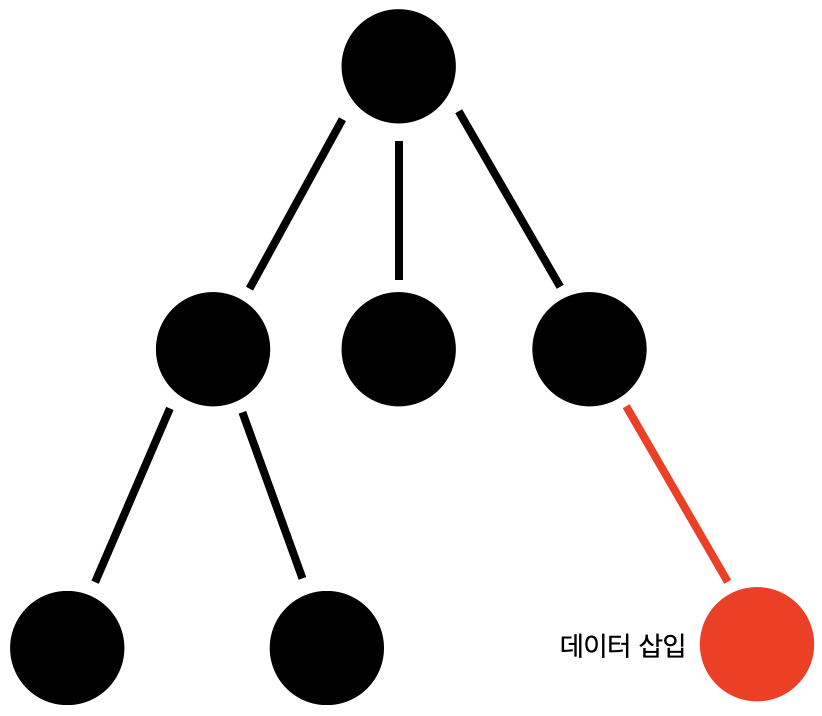
이러한 트리에 데이터를 삽입할려면 어떻게 해야할까요? 자료크기에 상관없이 노드를 지정하여 삽입하면 되기때문에 빅오는 O(1)입니다. (트리에서 데이터 추가는 삽입과 동일합니다.)
데이터를 찾을 때, 루트노드부터 탐색해야 되기 때문에 빅오는 O(n)이 됩니다.
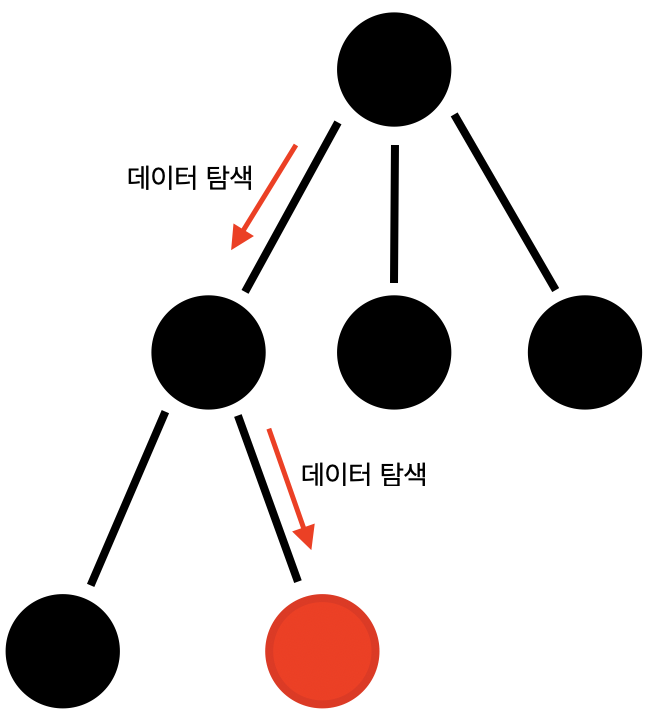
데이터 삭제를 위해, 데이터가 담긴 노드를 찾은 후 삭제해야 되기 떄문에 빅오는 O(n)이 됩니다.
• 일반 트리 코드
- 트리는 value, children 속성과 add, remove, contain 메소드를 가집니다. - children 또한 트리입니다.
//JavaScript
function Tree (value) {
const tree = {};
tree.value = value;
tree.children = [];
tree.addChild = function (value) {
tree.children.push(Tree(value));
}
tree.contain = function (target) {
if (target === this.value) {
return true;
}
for (let i = 0; i < this.children.length; i++) {
if (this.children[i].contain(target)) {
return true;
}
}
return false;
}
tree.bfs = function () {
const search = [];
const queue = [];
queue.push(tree);
while(queue.length) {
const currentNode = queue.shift();
queue.push(.currentNode.children);
search.push(currentNode.value);
}
return search;
}
tree.dfs = function () {
const search = [];
const stack = [];
stack.push(tree);
while(stack.length) {
const currentNode = stack.shift();
stack.unshift(.currentNode.children);
search.push(currentNode.value);
}
return search;
}
return tree;
}
이진 트리 (Binary Tree)
두개 이하의 자식노드를 가지고 있는 트리를 이진트리로 정의합니다. 아래 그림은 이진트리를 보여줍니다. 특별히 모든 레벨(계층 깊이)이 노드로 가득 차있는 트리를 포화 이진 트리(Full Binary Tree)라 부르며, 모든 노드가 두개의 자식 노드를 가지고 있는 트리를 완전 이진 트리(Complete Binary Tree)라 부릅니다.
• 이진 트리 순회
- 전위 순회 : 루트 노드를 먼저 순회합니다. (루트 노드 → 왼쪽 노드 → 오른쪽 노드) - 중위 순회 : 루트 노드를 중간에 순회합니다. (왼쪽 노드 → 루투 노드 → 오른쪽 노드) - 후위 순회 : 루트 노드를 마지막에 순회합니다. (왼쪽 노드 → 오른쪽 노드 → 루트 노드)
• 빅오
이진트리의 삽입/탐색/삭제의 빅오는 일반트리와 동일합니다.
• 이진 트리 코드
- 트리는 value, left, right 속성과 addChild, contain, remove 메소드를 가집니다.
- left / value 또한 이진트리입니다.
//JavaScript
function BinaryTree (value) {
const binaryTree = {};
binaryTree.value = value;
binaryTree.left = null;
binaryTree.right = null;
binaryTree.addChild = function () {};
binaryTree.contain = function () {};
binaryTree.remove = function () {};
return binaryTree;
}
이진 탐색 트리 (Binary Search Tree)
탐색을 위해, 특정 조건을 가지고 이진 트리를 만든 것을 이진 탐색 트리라 합니다. 이진 탐색 트리는 아래와 같은 특징이 있습니다.
- 노드 값은 유일합니다.
- 왼쪽 노드는 부모노드보다 작습니다.
- 오른쪽 노드는 부모노드보다 큽니다.
• 예시
- Searching in an ordered data
• 빅오
이진 탐색 트리의 삽입/탐색/삭제의 빅오는 균형트리에서 log(n), 불균형트리에서 n입니다.
AVL 트리
AVL 트리는 스스로 균형을 잡는 이진탐색트리입니다. 발명자인 아델손 벨스키(Georgy Adelson-Velsky)와 에브게니 란디스(Evgenil Landis)의 이름을 따왔으며, 이진탐색트리에서 왼쪽과 오른쪽의 높이차가 1보다 커지면, 노드들을 재구성(회전)하여 양쪽 높이의 균형을 잡습니다. 이를 통해 이진탐색트리를 균형트리로 만들 수 있습니다.
빅오
AVL트리는 균형트리이기 때문에, 삽입/탐색/삭제의 빅오는 log(n)입니다.