자료구조 - 해시 테이블

테이블

테이블(맵)이란 key(중복되지 않는 key) - value가 하나의 쌍을 이루어 저장되어 있는 자료구조를 의미합니다. 테이블은 key를 통해 데이터를 다루기 때문에, 데이터 개수에 상관 없이 삽입, 삭제, 탐색의 빅오는 O(1)입니다. 하지만, 테이블은 key를 인덱스로하여 데이터를 저장하기 때문에 데이터 개수는 적을지라도 메모리 공간을 많이 차지 합니다.

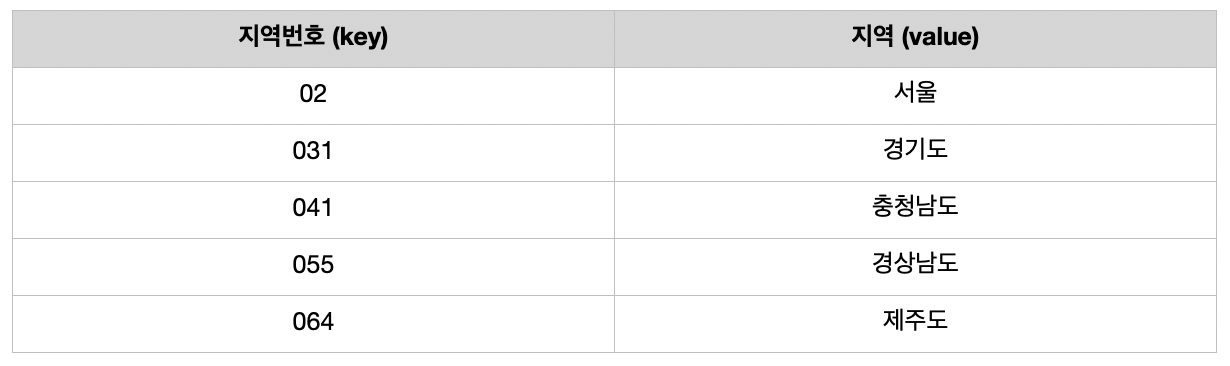
아래는 테이블의 예시입니다. 5개의 데이터를 저장하기 위해서 65개(0~64)의 메모리 공간을 차지할뿐더러, key가 흔히 쓰는 인덱스(0, 1, 2)와 달라 적절해 보이지 않습니다. (배열의 인덱스는 0부터 시작하기 때문에 65개의 공간을 차지합니다.)

이러한 문제의식으로부터 해시테이블이 만들어지게 되었습니다.

해시테이블

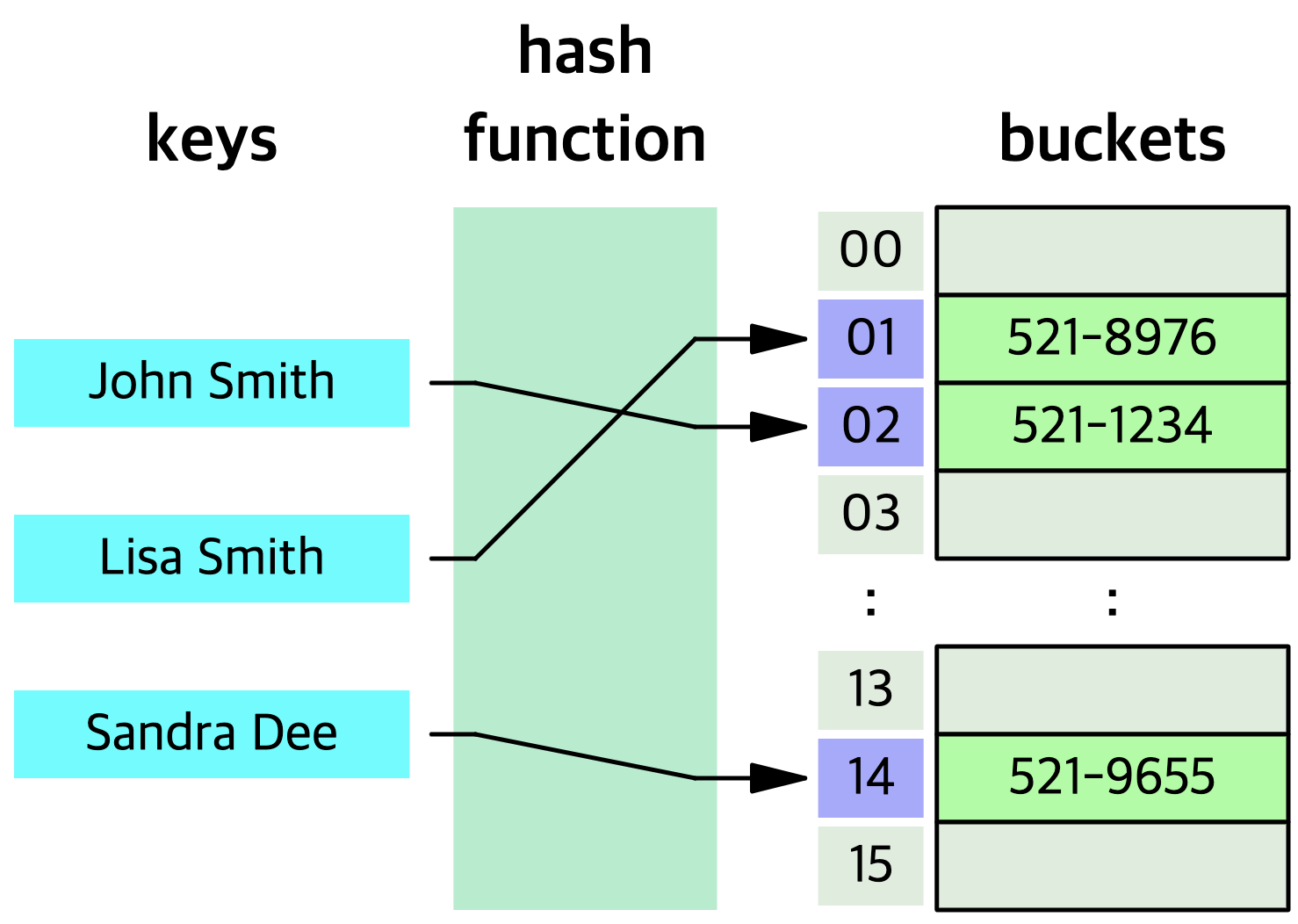
해시테이블이란 해시함수가 만든 해시코드를 key로 갖는 테이블을 의미합니다.

• 해시함수

해시함수는 임의의 길이의 데이터를 고정된 길이의 데이터로 매핑해주는 함수입니다. 해시함수에서 얻어지는 값을 해시코드라 합니다.

해시함수 조건 - 결정성(Deterministic) : 해시함수는 동일한 키에 대해 동일한 해시코드를 생성해야합니다.
- 효율성(Efficiency) : 시간복잡도가 O(1)이어야 합니다.
- 균일성(Uniform Distribution) : 메모리 공간의 효율적 사용 및 충돌을 줄이기 위해, 해시코드는 고르게 분포해야합니다.

• 해시코드 충돌

임의의 길이의 데이터를 고정된 길이의 데이터로 바꾸기 때문에, 필연적으로 해시코드 충돌은 발생할 수 밖에 없습니다. 이처럼 해시코드 충돌이 발생했을때, 기존 해시코드를 피하여 데이터를 저장하는 방법은 아래와 같습니다.

개방 주소법 (Open Addressing)
- 선형 탐사(Linear Probing) : 충돌해시코드의 +1의 인덱스에 데이터를 저장합니다. 만일 다른 데이터가 이미 저장되어 있다면, 다시 +1을 하여 저장합니다.

- 이차 탐사(Quadratic Probin) : 선형 탐사는 충돌해시코드 옆에 데이터를 저장하기 때문에, 데이터가 밀집되는 문제가 있습니다. 이러한 군집 문제를 해결하기 위해 +1대신 충돌해시코드²을 하여 데이터를 저장합니다.

- 재해싱 / 이중 해싱 : 충돌해시코드를 해싱하여 해시코드를 재생성합니다.

분리 연결법 (Separate Chaining)
- 충돌해시코드에 연결리스트를 만들어 데이터를 저장합니다.

• 예시

- Address Book - Dictionary - Block Chain

• 빅오

해시테이블은 key로 데이터를 다루기 때문에, 삽입/탐색/삭제의 빅오는 O(1)입니다. 다만, 충돌해시코드의 경우 삽입/탐색/삭제는 O(n)이 될 수 있습니다.

해시테이블은 자료처리가 O(1)이라 좋아보이지만, 아래와 같은 제한사항이 있습니다.

• 좋은 해시함수를 가져야 합니다.
• 데이터 개수에 비해 큰 메모리 공간을 차지합니다.
• 정렬된 데이터를 저장하는데 적합하지 않습니다.