정렬

정렬

정리된 자료에서 값을 찾는것이, 정리되지 않은 자료에서 찾는것보다 효율적입니다. 이처럼 정렬이란 자료의 효율적인 관리를 위해, 자료를 어떤 기준에 따라 배치하는 것을 의미합니다. 시각화 된 자료를 통해 정렬에 대한 이해도를 높일 수 있습니다. 다음은 정렬(Sort)의 종류입니다.

• 버블 정렬
• 삽입 정렬
• 선택 정렬
• 빠른 정렬
• 병합 정렬
• 빠른 선택
• 계수 정렬

아래에서 각 정렬에 대해 자세히 살펴보겠습니다.

버블 정렬 (Bubble Sort)

버블 정렬은 제일 기본적인 정렬 알고리즘입니다. 전체 배열을 순회하며, 인접한 두 요소를 기준(오름차순/내림차순)에 따라 비교 및 교환하여 정렬합니다. 아래는 오름차순으로 정렬하는 버블 정렬의 도식도입니다. 도식도를 보면, 자료를 순회하며 오름차순으로 정렬되고 있습니다.

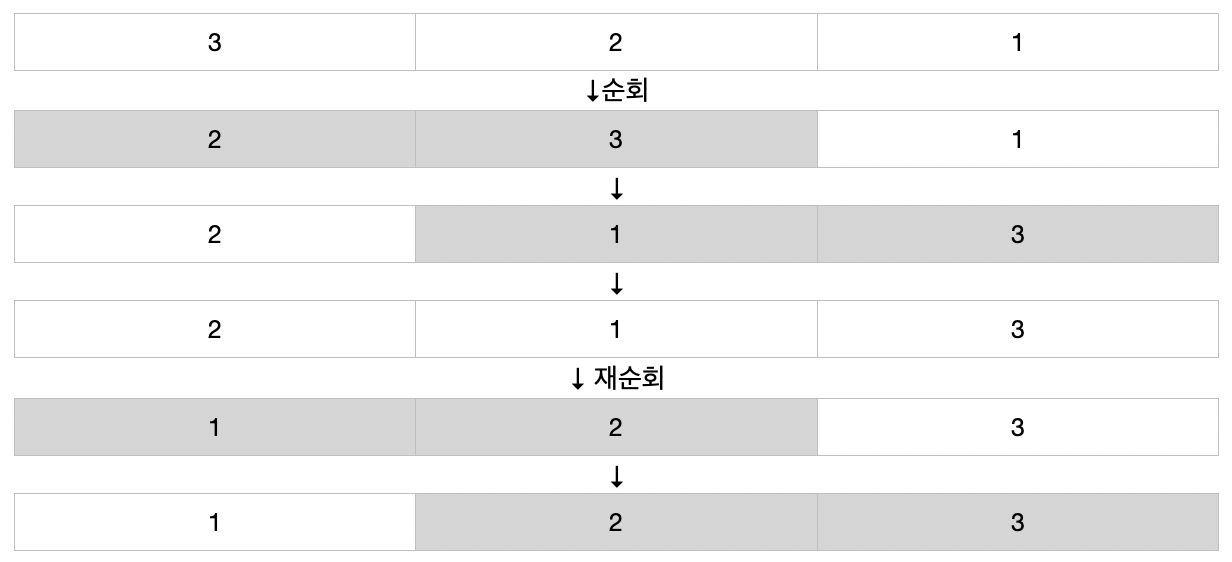
특성

n개의 요소가 있을때, 자료를 순회하며 하나의 요소를 기준에 맞게 정렬시킵니다(맨 오른쪽에 제일 큰 요소를 위치시키며, 다음 순회에서는 맨 오른쪽의 왼쪽에 그 다음으로 큰 요소를 위치시킵니다., 즉 한번 순회에 남은 요소 중 제일 큰 요소를 올바른 위치에 정렬시킵니다.). 이 과정을 n개의 요소에 대해 반복하므로 버블정렬의 시간복잡도 빅오는 O(n²)이 됩니다. 다만 정렬된 자료에 대해서는 한번만 순회하면 되기 때문에, 최적화된 버블 정렬 알고리즘을 사용한다면 빅오는 O(n)이 됩니다. 버블 정렬은 별도의 공간을 요구하지 않아 In Place이며, 공간복잡도 빅오는 O(1)입니다. 또한 정렬 후 중복된 값은 원래 자료와 순서가 동일하기 때문에 안정(Stable) 정렬입니다.

버블 정렬 코드

// JavaScript
function bubbleSort(data) {
  for (let i = 0; i < data.length; i++) {
    for (let j = 0; j < data.length - i - 1; j++) {
      if (data[i] > data[i + 1]) {
        const temp = data[i];
        data[i] = data[i + 1];
        data[i + 1] = data[i];
      }
    }
  }
  return data;
}

삽입 정렬 (Insertion Sort)

삽입 정렬 또한 기본적인 정렬 알고리즘입니다. 정렬될 요소가 앞의 요소들과 기준(오름차순/내림차순)에 맞게 비교되어 알맞는 위치에 삽입되어 들어갑니다. 아래는 오름차순으로 정렬하는 삽입 정렬의 도식도입니다. 도식도를 보면, 자료를 순회하고 앞 요소들과 비교하여 요소를 위치에 맞게 삽입하고 있습니다.

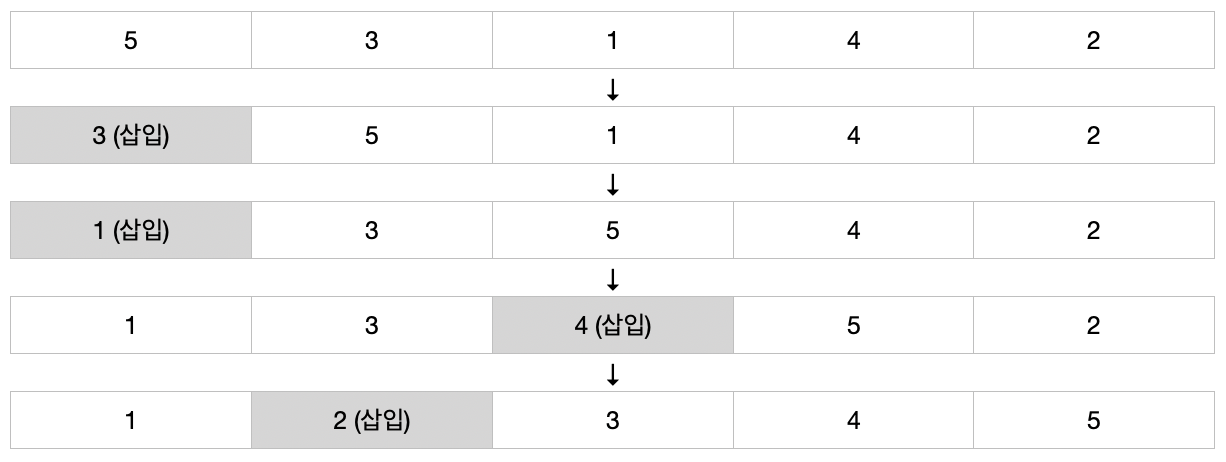
특성

n개의 요소가 있을때, 자료를 순회하며 하나의 요소를 기준에 맞게 삽입합니다. (해당 요소의 왼쪽을 탐색하며 삽입될 공간을 찾으며, 그 결과 왼쪽은 정렬된 상태이기에 원배열이 변경되어도 관계없습니다. 즉, 한번 순회에 왼쪽을 정렬시킵니다.) 이 과정에서 요소 하나를 삽입하기 위해 앞부분을 순회 및 비교하므로 삽입정렬의 시간복잡도 빅오는 O(n²)이 됩니다. 다만 이미 정렬된 자료에 대해서는 시간복잡도 빅오는 O(1)입니다. 삽입 정렬은 별도의 공간을 요구하지 않아 제자리(In Place) 정렬이며, 공간복잡도 빅오는 O(1)입니다. 또한 정렬 후 중복된 값은 원래 자료와 순서가 동일하기 때문에 안정(Stable) 정렬입니다.

삽입 정렬 코드

// JavaScript
function insertionSort (data) {
  for (let i = 0; i < data.length; i++) {
    let j = i;

    while (data[j] > data[j - 1] && j > 0) {
      const temp = data[j];
      data[j] = data[j - 1];
      data[j - 1] = temp;
      j--;
    }
  }

  return data;
}

선택 정렬 (Selection Sort)

선택 정렬은 기준(오름차순-최소값/내림차순-최대값)에 맞는 요소를 선택해 현재 위치에 놓음으로써, 배열을 정렬하는 알고리즘입니다. 아래는 오름차순으로 정렬하는 선택 정렬의 도식도입니다. 도식도를 보면 최소값이 현재 위치에 놓이게 함으로써, 오름차순으로 정렬되게 합니다.

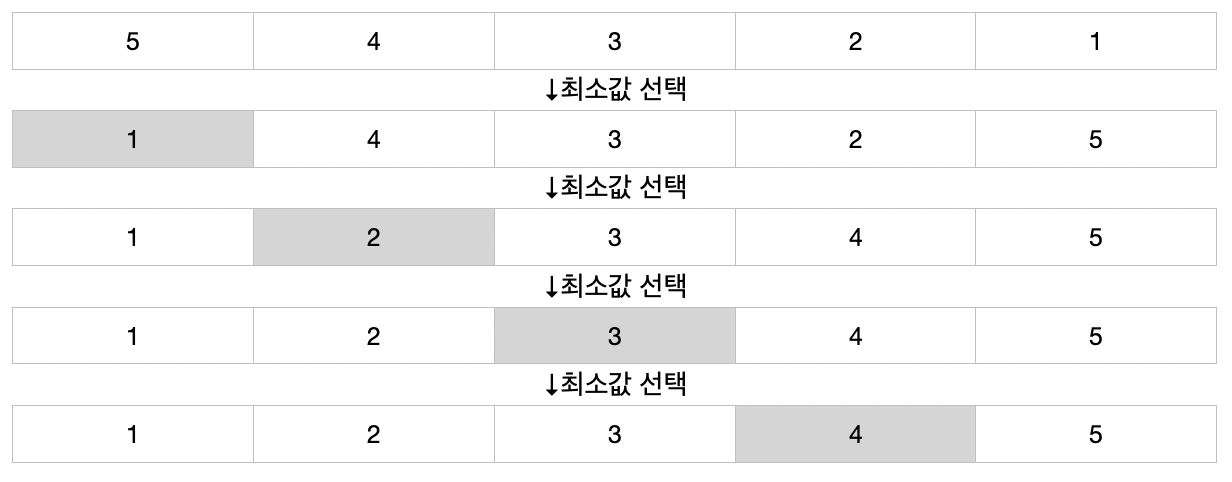
특성

n개의 요소가 있을때, 현재 위치에 맞는 요소를 선택하기 위해 자료를 순회해야하며, 이를 n개의 위치에 반복해야하므로, 선택정렬의 시간복잡도 빅오는 O(n²)이 됩니다. (선택정렬은 순회 횟수가 고정되어 있어 평균, 최선, 최악의 경우에도 O(n²) 입니다.) 선택 정렬은 별도의 공간을 요구하지 않아 제자리(In Place)정렬이며, 공간복잡도 빅오는 O(1)입니다. 또한 정렬 후 중복된 값은 원래 자료와 순서가 동일하지 않기 때문에 불안정(Unstable)정렬입니다.

선택 정렬 코드

//JavaScript
function selectionSort (data) {
  for (let i = 0; i < data.length - 1; i++) {
    let minIndex = i;

    for (let j = i + 1; j < data.length; j++) {
      if (data[j] < data[minIndex]) {
        minIndex = j;
      }
    }

    if (data[i] !== data[minIndex]) {
      const temp = data[i];
      data[i] = data[minIndex];
      data[minIndex] = temp;
    }
  }

  return data;
}

빠른 정렬 (Quick Sort)

빠른 정렬은 분할정복(Divide and Conquer) 정렬 알고리즘입니다. 기준점(Pivot)을 기준으로 왼쪽은 작은 요소들, 오른쪽은 큰 요소들로 자료를 정렬합니다. 정렬된 자료를 기준점으로 나누고 앞서 했던 과정을 요소가 하나 남을때까지 반복합니다. 이러한 재귀적 과정을 통해 자료를 정렬할 수 있습니다.

특성

빠른 정렬의 시간 복잡도는 O(nlog(n))입니다. 하지만 기준점을 잘 못 선정(기준점을 최대값이나 최소값으로 선정)할 경우 O(n²)이 됩니다. 빠른 정렬은 재귀함수의 콜스택을 위한 메모리 공간이 필요하므로 공간 복잡도는 O(nlog(n))입니다. 또한 정렬 후 중복된 값은 원래 자료와 순서가 동일하지 않기 때문에 불안정(Unstable) 정렬입니다.

빠른 정렬 코드

//JavaScript
function quickSort (data, left, right) {
  const index = partition(data, left, right);

  if (index - 1 > left) {
    quickSort(data, left, index - 1);
  }

  if (index < right) {
    quickSort(data, index, right);
  }

  return data;
}

function partition (data, left, right) {
  let _left = left;
  let _right = right;
  const pivot = data[Math.floor((_left + _right) / 2)];

  while (_left <= _right) {
    let temp;

    if (_left + 1 >= _right) {
      _left = left;
      _right = right;
    }

    while (data[_left] < pivot) {
      _left++;
    }

    while (data[_right] > pivot) {
      _right--;
    }

    if (_left <= _right) {
      temp = data[_left];
      data[_left] = data[_right];
      data[_right] = temp;
      _left++;
      _right--;
    }
  }

  return _left;
}

quickSort([1, 5, 7, 2, 1, 8, 9], 0, [1, 5, 7, 2, 1, 8, 9].length - 1);

병합 정렬 (Merge Sort)

병합 정렬은 분할정복(Divide and Conquer) 정렬 알고리즘입니다. 자료를 요소가 하나가 될 때까지 분할한 후, 분할된 자료를 정렬하여 병합합니다. 이 과정을 원래 자료가 될 때까지 반복합니다. 이러한 재귀적 과정을 통해 자료를 정렬할 수 있습니다.

특성

병합 정렬의 시간 복잡도는 O(nlog(n))입니다. (병합정렬은 재귀 횟수가 고정되어 있어 평균, 최선, 최악의 경우에도 O(nlon(n)) 입니다.) 병합 정렬은 분할된 요소들을 저장할 공간이 필요하므로 공간 복잡도는 O(n)입니다. 또한 정렬 후 중복된 값은 원래 자료와 순서가 동일하기 때문에 안정(Stable) 정렬입니다.

병합 정렬 코드

//JavaScript
function mergeSort (data) {
  if (data.length === 1) {
    return data;
  }

  const midpoint = Math.floor(data.length / 2);
  const leftData = data.slice(0, midpoint);
  const rightData = data.slice(midpoint);

  return merge(mergeSort(leftData), mergeSort(rightData));
}

function merge (leftData, rightData) {
  const mergedData = [];
  let leftDataIndex = 0;
  let rightDataIndex = 0;

  while (leftDataIndex < leftData.length && rightDataIndex < rightData.length) {
    if (leftData[leftDataIndex] > rightData[rightDataIndex]) {
      mergedData.push(rightData[rightDataIndex++]);
    } else {
      mergedData.push(leftData[leftDataIndex++]);
    }
  }

  const leftDataRemains = leftData.slice(leftDataIndex);
  const rightDataRemains = rightData.slice(rightDataIndex);

  return mergedData.concat(leftDataRemains).concat(rightDataRemains);
}

mergeSort([8, 5, 7, 4, 2]));